希尔排序、归并排序、快速排序、堆排序 (原创)

1、希尔排序

package com.tingcream.alg.sort;
 
/**
 * 希尔排序 ： 分组+插入排序
 */
public class Shell {
 
    /**
     * 1、对整个数组按步长h进行分组
     *   h的值初始值可这样得出
     *    int h=1;
     *    while(h<a.length/2){
     *             h=2*h+1;
     *     }
     * 2、对每个分组进行插入排序。每完成一轮，让h值减半再执行步骤1，直到h<1为止
     *
     */
    public static void sort(Comparable[] a){
 
        //初始化h值为1
        int h=1;
        //修正h的值
        while(h<a.length/2){
            h=2*h+1;
        }
 
        while(h>=1){
            //找到待插入的元素
            for(int i=h;i<a.length;i++){
                //把待插入的元素插入到有序数列中
                for(int j=i;j>=h;j-=h){
                    if(gt(a[j-h],a[j])){
                        swap(a,j-h,j);
                    }else{
                        break;
                    }
                }
            }
            //减小h的值,直到h<1
            h=h/2;
        }
    }
 
 
 
    //判断a是否大于b
    public static boolean gt(Comparable a,Comparable b){
        return a.compareTo(b)>0;
    }
    //交换数组的两个元素
    private static  void swap(Comparable[] arr,int i,int j){
        Comparable temp;
        temp=arr[i];
        arr[i]=arr[j];
        arr[j]=temp;
    }
}

2、快速排序

package com.tingcream.alg.sort;
 
/**
 * 快速排序 （不稳定排序算法）
 *
 *  最好情况 O(nlogn)
 *  平均情况 O(nlogn)
 *  最坏情况 O(n^2)
 *
 */
public class Quick {
 
   //对数组内的元素进行排序
    public   static void sort(Comparable[] arr){
        int lo=0;
        int hi=arr.length-1;
        sort(arr,lo,hi);
    }
 
    //对数组arr中从索引lo到索引hi之间的元素进行排序
    public static void sort(Comparable[] arr,int lo,int hi){
        //安全性校验
        if(hi<=lo){
            return ;
        }
        //需要对数组中lo索引到hi索引的元素进行分组 （左子组、右子组）
        int partition=partition(arr,lo,hi);//返回的是分界值的索引（位置变换后）
 
        //让左子组有序
        sort(arr,lo,partition-1);
 
        //让右子组有序
        sort(arr,partition+1,hi);
 
    }
 
 
    //对数组arr中，从索引lo到索引hi之间的元素进行分组，并返回分组界限对应的索引
    public static int partition(Comparable[] a,int lo,int hi){
        Comparable key=a[lo];//得到分界值
        int left=lo;
        int right=hi+1;
 
        //切分
        while(true){
            //先看right指针
            while(less(key,a[--right])){
                if(right==lo){
                    break;
                }
 
            }
            //再看left指针
            while(less(a[++left],key)){
                if(left==hi){
                    break;
                }
            }
            //判断left>=right ，如果是说明扫描完毕，结束循环。如果不是交换元素即可
            if(left>=right){
                break;
            }else{
                swap(a,left,right);
            }
        }
        swap(a,lo,right);
        return right;
    }
 
 
    //判断a是否小于b
    public static boolean  less(Comparable a,Comparable b){
        return a.compareTo(b)<0;
    }
 
 
    //交换数组的两个元素
    private  static void swap(Comparable[] arr,int i,int j){
        Comparable temp;
        temp=arr[i];
        arr[i]=arr[j];
        arr[j]=temp;
    }

}

package com.tingcream.alg.sort;
 
/**
 * 归并排序
 *
 */
public class Merge {
   private  Comparable[] assist;
 
 
    /**
     * 排序
     * @param arr
     */
   public   void sort(Comparable[] arr){
       assist=new Comparable[arr.length];
       int lo=0;
       int hi=arr.length-1;
       sort(arr,lo,hi);
   }
 
    /**
     * 排序  对数组中的下标位置lo到下标位置hi 部分进行排序
     * @param arr
     * @param lo
     * @param hi
     */
   public void sort(Comparable[] arr,int lo,int hi){
       //安全性校验
       if(hi<=lo){
           return ;
       }
 
       int mid=lo +(hi-lo)/2;
       sort(arr,lo,mid);
       sort(arr,mid+1,hi);
 
       merge(arr,lo,mid,hi);
   }
 
    /**
     * 归并 （将分组进行归并 排序）
     * @param arr  数组
     * @param lo   下标(低)
     * @param mid   下标(中)
     * @param hi   下标(高)
     */
   private void merge(Comparable[] arr,int lo,int mid,int hi){
 
 //定义三个指针 p(指向辅助数组lo位置), p1 (指向左子组lo位置),p2(指向右子组mid+12位置)
//遍历，移动p1和p2指针。比较p1指向的值和p2指向的值哪个小，把较小的值放入辅助数组中
//遍历，如果最后p1的指针没有走完，那么顺序移动p1指针，把对应的元素放入到辅助数组中
//遍历，如果最后p2的指针没有走完，那么顺序移动p2指针，把对应的元素放入到辅助数组中
//把整个辅助数组中的元素拷贝到原数组中
 
 
       int  p=lo;
       int p1=lo;
       int p2=mid+1;
 
       //遍历，移动p1和p2指针。比较p1指向的值和p2指向的值哪个较小，把较小的值放入辅助数组中
       while(p1<=mid && p2<=hi){
           if(lt(arr[p1],arr[p2])){
               assist[p++]=arr[p1++];
           }else{
               assist[p++]=arr[p2++];
           }
 
       }
 
       while(p1<=mid){
           assist[p++]=arr[p1++];
       }
 
       while(p2<=hi){
           assist[p++]=arr[p2++];
       }
 
       //把整个辅助数组中的元素拷贝到原数组中
       for(int k=lo;k<=hi; k++){
           arr[k]=assist[k];
       }
 
   }
 
 
 
    //判断a是否小于b
    public  boolean lt(Comparable a,Comparable b){
        return a.compareTo(b)<0;
    }
 
    //交换数组的两个元素
    private   void swap(Comparable[] arr,int i,int j){
        Comparable temp;
        temp=arr[i];
        arr[i]=arr[j];
        arr[j]=temp;
    }

}

4、堆排序

package com.tingcream.alg.heap;
 
/**
 * 堆排序  (数组)
 */
public class HeapSort {
 
 
    //对数组中的数据从小到大排序
    public static void sort(Comparable[] source){
 
        //定义一个变量，记录未排序的元素中的最大索引
        //通过循环，交换1索引处的元素和排序的元素中的最大索引出的元素
        //排序交换后的最大索引所在的索引，让它不要参与堆的下沉调整
        //需要对索引1出的元素进行堆的下沉调整
 
        //创建堆
        Comparable[] heap=new Comparable[source.length+1];
        createHeap(source,heap);//得到堆heap
 
        int N=heap.length-1;
        while(N!=1){
            //交换元素
            exchange(heap,1,N);
            N--;
            sink(heap,1,N);
        }
        //将新数组中所有元素复制到原数组
        System.arraycopy(heap,1,source,0,source.length);
 
    }
 
 
 
    //根据原数组构造出推
    private static void createHeap(Comparable[] source,Comparable[] heap){
        System.arraycopy(source,0,heap,1,source.length);//系统native方法 完成数组复制
        //把source中元素拷贝到heap中，heap中的元素就形成了一个无序的堆
        //对堆中的元素做下沉调整 （从长度的一半出，往索引1处扫描）
        for(int i=(heap.length)/2;i>0;i--){
            sink(heap,i,heap.length-1);
        }
 
    }
 
 
 
    //在heap堆中，对k处的元素进行下沉，范围是0~range  ,2*k的值不能大于range值
    private static void sink(Comparable[] heap,int k,int range){
        while(2*k<=range) {
            //较大值的索引
            int max;
            //找到当前节点的左右子节点中值较大的值
            if (2*k+1<=range) {//如果存在右子结点
                if (less(heap,2*k,2*k+1)) {
                    max=2*k+1;
                } else {
                    max=2*k;
                }
            } else {//如果不存在右子结点
                max=2*k;
            }
            if(less(heap,max,k)){
                break ;
            }
            exchange(heap,k,max);
            k=max;
        }
    }
    private static boolean less(Comparable[] a,int i,int j){
        return a[i].compareTo(a[j])<0;
    }
 
    private static void exchange(Comparable[] a,int i,int j){
        Comparable tmp=a[i];
        a[i]=a[j];
        a[j]=tmp;
    }
}

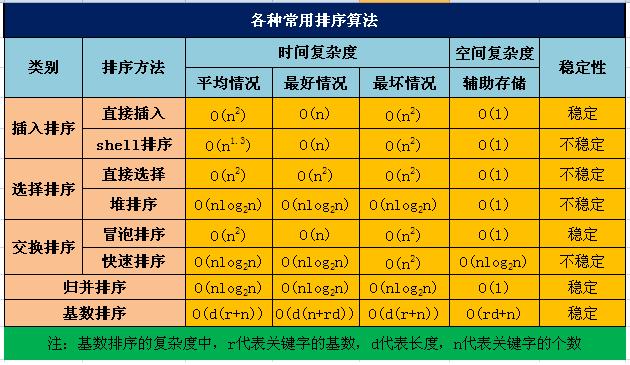
希尔排序、快速排序 、归并排序、堆排序 都是高级排序算法
这4种排序算法中，只有归并排序是稳定排序，其他3种都是不稳定排序。
快速排序算法的最好情况复杂度和平均复杂度都是 O(nlogn)，最坏情况是O(n^2)，不稳定
堆排序，最好情况、平均情况、最坏情况都是O(nlogn) ，不稳定
希尔排序，不稳定，采用事后分析法得出的结论是，排序效率极高，有时比快速排序更快。但是平均来看，快速排序在实际中仍然是最快的排序算法。